The iPhone has an accelerometer in it, which is a neat little bit of tech which has various uses. When your phone switches between portrait and landscape mode, that’s the accelerometer, and when you shake your phone, that’s the accelerometer as well.
One thing that I’m sure you’ve seen on an iPhone or iPod add somewhere is some sort of driving game where you hold the device on both sides and move it like a steering wheel to turn the car. I recently had an instance where I was asked to do this (although there are no cars involved).
It turns out that it’s a little bit more complex that you would imagine at first, but at the same time wonderfully simple once you’ve got it. In true hacker style I didn’t actually read any of the documentation for this, which probably would have helped. Once I couldn’t find anything useful on google I resorted to reverse engineering the values and inferring what was going on.
I wanted the device’s position, not it’s movements, so I started with some code from Apple’s developer’s centre which gives you the result of using a low pass filter on the raw accelerometer values. This means we get rid of the higher frequencies (movements) and just get more or less static values.
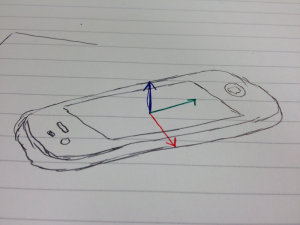
So, once I worked out which value I wanted to use, I could calculate the angle of the device when held vertically in landscape mode (image to the right).
All I needed for this was the inverse sine of the y-axis (green) value. The y-axis is the one that runs from the speaker end to the microphone end of an iPhone along the long edge of the screen. Piece of cake.
Because it’s easier to work with degrees, I did that rather than sticking with radians, so my equation came out as
\[\begin{aligned}
\frac{180 \cdot \sin^{-1}(y)}{\pi}.
\end{aligned} \]
This is where it gets tricker. The accelerometer relies on gravity to take its readings on position, the values you get out of (for instance) the low-pass filter are the sin() of the angle between that axis and the horizontal.
This means that the accelerometer isn’t able to distinguish positions which only differentiate by a rotation around the vertical. To bring this back to our steering wheel concept, you can’t steer like a truck driver (image to the left).
This also presents another issue, since the accelerometer effectively measures angles with respect to the horizontal, you can’t use the same function to get a steering wheel rotation when the device is tilted towards the user – or away from them, but who would do that?
When the device is tilted toward the user, the y-axis will still be parallel to the horizontal when it’s not steered to the left or right, but it will never make it to a full 90 degrees from the horizontal (e.g. vertical). In this case I needed to know that, from a steering point of view, the device had been rotated the full 90 degrees.
This can be done using an axis which measures tilt towards or away from the user, I used the z-axis (blue), although it would be possible to use the x-axis (red) instead. The z-axis is the one coming straight out of the screen, horizontal to the plane of the device.
So, now we create our z-modifier, in order to avoid unnecessary conversions, this was left in radians (and it cancels out a bit better later on). What we need is a value that will leave our y-axis angle as is when the device is in landscape mode, but increases the reading on the y-axis angle when the phone is tilted. This works out as
\[\begin{aligned}
\frac{\pi}{\pi – 2 \cdot |sin^{-1}(z)|}
\end{aligned} \]
So, we multiply them together, cancel a couple of instances of pi and we’re left with
\[\begin{aligned}
\frac{180 \cdot \sin^{-1}(y)}{\pi – 2 \cdot |sin^{-1}(z)|}.
\end{aligned} \]
(180 * arcsin(y))/(pi – 2 * |arcsin(z)|)
Of course, what every programmer wants is the code, and it does turn out to be dead simple. Start with the filter class from Apple’s Accelerometer Graph sample code and just add the following method to the filter.
[objc]
– (double)steeringAngle
{
if ((M_PI-2*fabs(asin(self.z))) == 0)
// The device is horizontal, we’ll just set the angle to 0 by convension:
steeringAngle = 0.0f;
else
steeringAngle = (asin(self.y)*180/(M_PI-2*fabs(asin(self.z))));
return steeringAngle;
}
[/objc]